
Chapter 3
Defining Functions and Constants
|
|
In this Chapter we explain how functions (actually: graph rewrite rules) and constants (actually: graph expressions) are defined in Clean. The body of a function consists of an (root) expression (see 3.4). With help of patterns (see 3.2) and guards (see 3.3) a distinction can be made between several alternative definitions for a function. Functions and constants can be defined locally in a function definition. For programming convenience (forcing evaluation, observation of unique objects and threading of sequencial operations) a special let construction is provided (see 3.5.1). The typing of functions is discussed in Section 3.7. For overloaded functions see Chapter 6. For functions working on unique datatypes see Chapter 9.
3.1 Functions
|
FunctionDef |
= |
[FunctionTypeDef] |
|
|
|
|
DefOfFunction |
|
|
DefOfFunction |
= |
{FunctionAltDef ;}+ |
|
|
FunctionAltDef |
= |
Function {Pattern} |
|
|
|
|
{LetBeforeExpression} |
// see 3.5.4 |
|
|
|
{{| Guard} =[>] FunctionBody}+ |
|
|
|
|
[LocalFunctionAltDefs] |
// see 3.5 |
|
Function |
= |
FunctionName |
// ordinary function |
|
|
| |
(FunctionName) |
// operator function used prefix |
|
FunctionBody |
= |
RootExpression ; |
// see 3.4 |
|
|
|
[LocalFunctionDefs] |
// see 3.5 |
A function definition consists of one or more definition of a function alternative (rewrite rule). On the left-hand side of such a function alternative a pattern can be specified which can serve a whole sequence of guarded function bodies (called the rule alternatives) The root expression (see 3.4) of a particular rule alternative is chosen for evaluation when
• the patterns specified in the formal arguments are matching the corresponding actual arguments of the function application (see 3.2) and
• the optional guard (see 3.3) specified on the right-hand side evaluates to True.
The alternatives are tried in textual order. A function can be preceded by a definition of its type (Section 3.7).
 Function definitions are only allowed in implementation modules (see 2.3).
Function definitions are only allowed in implementation modules (see 2.3).
 It is required that the function alternatives of a function are
textually grouped together (separated by semi-colons when the layout sensitive
mode is not chosen).
It is required that the function alternatives of a function are
textually grouped together (separated by semi-colons when the layout sensitive
mode is not chosen).
 Each alternative of a function must start with the same function
symbol.
Each alternative of a function must start with the same function
symbol.
 A function has a fixed arity, so in each rule the same number of
formal arguments must be specified. Functions can be used curried and applied
to any number of arguments though, as usual in higher order functional
languages.
A function has a fixed arity, so in each rule the same number of
formal arguments must be specified. Functions can be used curried and applied
to any number of arguments though, as usual in higher order functional
languages.
 The function name must in principle be different from other names in
the same name space and same scope (see 2.1).
However, it is possible to overload functions and operators (see Chapter 6).
The function name must in principle be different from other names in
the same name space and same scope (see 2.1).
However, it is possible to overload functions and operators (see Chapter 6).
Example of function definitions in a Clean module.
module example // module header
import StdInt // implicit import
map:: (a -> b) [a] -> [b] // type of map
map f list = [f e \\ e <- list] // definition of the function map
square:: Int -> Int // type of square
square x = x * x // definition of the function square
Start:: [Int] // type of Start rule
Start = map square [1..1000] // definition of the Start rule
An operator is a function with arity two that can be used as infix operator (brackets are left out) or as ordinary prefix function (the operator name preceding its arguments has to be surrounded by brackets). The precedence (0 through 9) and fixity (infixleft, infixright, infix) that can be defined in the type definition (see 3.7.1) of the operators determine the priority of the operator application in an expression. A higher precedence binds more tightly. When operators have equal precedence, the fixity determines the priority.
 When an operator is used in infix position both arguments have to be present. Operators can be used in
a curried way, but then they have to be used as ordinary prefix functions.
When an operator is used in infix position both arguments have to be present. Operators can be used in
a curried way, but then they have to be used as ordinary prefix functions.
Operator definition.
(++) infixr 0:: [a] [a] -> [a]
(++) [] ly = ly
(++) [x:xs] ly = [x:xs ++ ly]
(o) infixr 9:: (a -> b) (c -> a) -> (c -> b)
(o) f g = \x = f (g x)
3.2 Patterns
A pattern specified on the left-hand side of a function definition specifies the formal arguments of a function. A function alternative is chosen only if the actual arguments of the function application match the formal arguments. A formal argument is either a constant (some data constructor with its optional arguments that can consist of sub-patterns) or it is a variable.
|
Pattern |
= |
[Variable =:] BrackPattern |
|
|
BrackPattern |
= |
(GraphPattern) |
|
|
|
| |
Constructor |
|
|
| |
PatternVariable |
|
|
|
|
| |
SpecialPattern |
|
|
|
| |
DynamicPattern |
|
|
|
|
|
|
|
GraphPattern |
= |
Constructor {Pattern} |
// Ordinary data constructor |
|
|
| |
GraphPattern ConstructorName GraphPattern |
// Infix data constructor |
|
|
| |
Pattern |
|
|
|
|
|
|
|
PatternVariable |
= |
Variable |
|
|
|
| |
_ |
|
A pattern variable can be a (node) variable or a wildcard. A variable is a formal argument of a function that matches on any concrete value of the corresponding actual argument and therefore it does not force evaluation of this argument. A wildcard is an anonymous variable ("_") one can use to indicate that the corresponding argument is not used in the right-hand side of the function. A variable can be attached to a pattern (using the symbol ‘=:’) that makes it possible to identify (label) the whole pattern as well as its contents. When a constant (data constructor) is specified as formal argument, the actual argument must contain the same constant in order to have a successful match.
Example of an algebraic data type definition and its use in a pattern match in a function definition.
::Tree a = Node a (Tree a) (Tree a)
| Nil
Mirror:: (Tree a) -> Tree a
Mirror (Node e left right) = Node e (Mirror right) (Mirror left)
Mirror Nil = Nil
Use of anonymous variables.
:: Complex :== (!Real,!Real) // synonym type def
realpart:: Complex -> Real
realpart (re,_) = re // re and _ are pattern variables
Use of list patterns, use of guards, use of variables to identify patterns and sub-patterns; merge merges two (sorted) lazy lists into one (sorted) list.
merge:: [Int] [Int] -> [Int]
merge f [] = f
merge [] s = s
merge f=:[x:xs] s=:[y:ys]
| x<y = [x:merge xs s]
| x==y = merge f ys
| otherwise = [y:merge f ys]
 It is possible that the specified patterns turn a function into a
partial function (see 3.7.3). When a partial
function is applied outside the domain for which the function is defined it
will result into a run-time error. A compile time warning is
generated that such a situation might arise.
It is possible that the specified patterns turn a function into a
partial function (see 3.7.3). When a partial
function is applied outside the domain for which the function is defined it
will result into a run-time error. A compile time warning is
generated that such a situation might arise.
The formal arguments of a function and the function body are contained in a new local scope.
![]() functionName args
= expression
functionName args
= expression
 All variable symbols introduced at the left-hand side of a function
definition must have different names.
All variable symbols introduced at the left-hand side of a function
definition must have different names.
For convenience and efficiency special syntax is provided to express pattern match on data structures of predefined type and record type. They are treated elsewhere (see below).
|
SpecialPattern |
= |
BasicValuePattern |
// see 4.1.2 |
|
|
| |
ListPattern |
// see 4.2.2 |
|
|
| |
TuplePattern |
// see 4.3.2 |
|
|
| |
ArrayPattern |
// see 4.4.2 |
|
|
| |
RecordPattern |
// see 5.2.2 |
3.3 Guards
|
Guard |
= |
BooleanExpr |
|
|
| |
otherwise |
A guard is a Boolean expression attached to a rule alternative that can be regarded as generalisation of the pattern matching mechanism: the alternative only matches when the patterns defined on the left hand-side match and its (optional) guard evaluates to True (see 3.1). Otherwise the next alternative of the function is tried. Pattern matching always takes place before the guards are evaluated.
The guards are tried in textual order. The alternative corresponding to the first guard that yields True will be evaluated. A right-hand side without a guard can be regarded to have a guard that always evaluates to True (the ‘otherwise’ or ‘default’ case). In keyword otherwise is synonym for True for people who like to emphasize the default option.
 Only the last rule alternative of a function can have otherwise as
guard or can have no guard.
Only the last rule alternative of a function can have otherwise as
guard or can have no guard.
 It is possible that the guards turn the function into a partial
function (see 3.6.3). When a partial function is applied outside the domain for which the function is defined it
will result into a run-time error. At compile time this cannot be
detected.
It is possible that the guards turn the function into a partial
function (see 3.6.3). When a partial function is applied outside the domain for which the function is defined it
will result into a run-time error. At compile time this cannot be
detected.
Function definition with guards.
filter:: Int [Int] -> [Int]
filter pr [n:str]
| n mod pr == 0 = filter pr str
| otherwise = [n:filter pr str]
Equivalent definition of previous filter.
filter:: Int [Int] -> [Int]
filter pr [n:str]
| n mod pr == 0 = filter pr str
= [n:filter pr str]
Guards can be nested. When a guard on one level evaluates to True, the guards on a next level are tried.
 To ensure that at least one of the alternatives of a nested guard
will be successful, a nested guarded alternative must always have a 'default
case' as last alternative.
To ensure that at least one of the alternatives of a nested guard
will be successful, a nested guarded alternative must always have a 'default
case' as last alternative.
Example of a nested guard.
example arg1 arg2
| predicate11 arg1 // if predicate11 arg1
| predicate21 arg2 = calculate1 arg1 arg2 // then (if predicate21 arg2
| predicate22 arg2 = calculate2 arg1 arg2 // elseif predicate22 arg2 then
| otherwise = calculate3 arg1 arg2 // else …)
| predicate12 arg1 = calculate4 arg1 arg2 // elseif predicate12 arg1 then …
3.4 Expressions
The main body of a function is called the root expression. The root expression is a graph expression.
|
RootExpression |
= |
GraphExpr |
|
GraphExpr |
= |
Application |
|
|
Application |
= |
{BrackGraph}+ |
|
|
|
| |
GraphExpr Operator GraphExpr |
|
|
|
| |
GenericAppExpr |
|
|
BrackGraph |
= |
GraphVariable |
|
|
|
| |
Constructor |
|
|
|
| |
Function |
|
|
|
| |
(GraphExpr) |
|
|
|
| |
LambdaAbstr |
// see 3.4.1 |
|
|
| |
CaseExpr |
// see 3.4.2 |
|
|
| |
LetExpr |
// see 3.5.1 |
|
|
| |
SpecialExpression |
|
|
|
| |
DynamicExpression |
|
|
Function |
= |
FunctionName |
|
|
| |
(FunctionName) |
|
Constructor |
= |
ConstructorName |
|
|
| |
(ConstructorName) |
|
Operator |
= |
FunctionName |
|
|
| |
ConstructorName |
|
GraphVariable |
= |
Variable |
|
|
| |
SelectorVariable |
An expression generally expresses an application of a function to its actual arguments or the (automatic) creation of a data structure simply by applying a data constructor to its arguments. Each function or data constructor can be used in a curried way and can therefore be applied to any number (zero or more) of arguments. A function will only be rewritten if it is applied to a number of arguments equal to the arity of the function (see 3.1). Function and constructors applied on zero arguments just form a syntactic unit (for non-operators no brackets are needed in this case).
 All expressions have to be of correct type (see Chapter 5).
All expressions have to be of correct type (see Chapter 5).
 All symbols that appear in an expression must have been defined
somewhere within the scope in which the expression appears (see 2.1).
All symbols that appear in an expression must have been defined
somewhere within the scope in which the expression appears (see 2.1).
 There has to be a definition for each node variable and selector
variable within in the scope of the graph expression.
There has to be a definition for each node variable and selector
variable within in the scope of the graph expression.
Operators are special functions or data constructors defined with arity two which can be applied in infix position The precedence (0 through 9) and fixity (infixleft, infixright, infix) which can be defined in the type definition of the operators determine the priority of the operator application in an expression. A higher precedence binds more tightly. When operators have equal precedence, the fixity determines the priority. In an expression an ordinary function application has a very high priority (10). Only selection of record elements (see 5.2.1) and array elements (see 4.4.1) binds more tightly (11). Besides that, due to the priority, brackets can sometimes be omitted; operator applications behave just like other applications.
 It is not allowed to apply operators with equal precedence in an
expression in such a way that their fixity conflict. So, when in a1 op1 a2 op2 a3 the operators op1 and op2 have the same precedence a conflict arises when op1 is defined as infixr implying that the expression must be read as a1 op1 (a2 op2 a3) while op2 is defined as infixl implying that the expression must be read as (a1 op1 a2) op2 a3.
It is not allowed to apply operators with equal precedence in an
expression in such a way that their fixity conflict. So, when in a1 op1 a2 op2 a3 the operators op1 and op2 have the same precedence a conflict arises when op1 is defined as infixr implying that the expression must be read as a1 op1 (a2 op2 a3) while op2 is defined as infixl implying that the expression must be read as (a1 op1 a2) op2 a3.
 When an operator is used in infix position both arguments
have to be present. Operators can be used in a curried way (applied to
less than two arguments), but then they have to be used as ordinary prefix
functions / constructors. When an operator is used as prefix function c.q.
constructor, it has to be surrounded by brackets.
When an operator is used in infix position both arguments
have to be present. Operators can be used in a curried way (applied to
less than two arguments), but then they have to be used as ordinary prefix
functions / constructors. When an operator is used as prefix function c.q.
constructor, it has to be surrounded by brackets.
There are two kinds of variables that can appear in a graph expression: variables introduced as formal argument of a function (see 3.1 and 3.2) and selector variables (defined in a selector to identify parts of a graph expression, see 3.6)
Example of a cyclic root expression. y is the root expression referring to a cyclic graph. The multiplication operator * is used prefix here in a curried way.
ham:: [Int]
ham = y
where y = [1:merge (map ((*) 2) y) (merge (map ((*) 3) y) (map ((*) 5) y))]
For convenience and efficiency special syntax is provided to create expressions of data structures of predefined type and of record type that is considered as a special kind of algebraic type. They are treated in elsewhere.
|
SpecialExpression |
=| |
BasicValue |
// see 4.1.1 |
|
|
| |
List |
// see 4.2.1 |
|
|
| |
Tuple |
// see 4.3.1 |
|
|
| |
Array |
// see 4.4.1 |
|
|
| |
ArraySelection |
// see 4.4.1 |
|
|
| |
Record |
// see 5.2.1 |
|
|
| |
RecordSelection |
// see 5.2.1 |
3.4.1 Lambda Abstraction
Sometimes it can be convenient to define a tiny function in an expression “right on the spot”. For this purpose one can use a lambda abstraction. An anonymous function is defined which can have several formal arguments that can be patterns as common in ordinary function definitions (see Chapter 3). However, only simple functions can be defined in this way: no guards, no rule alternatives, and no local definitions.
For compatibility with Clean 1.3 it is also allowed to use the arrow (‘->’) to separate the formal arguments from the function body:
|
LambdaAbstr |
= |
\ {Pattern} = GraphExpr |
|
|
| |
\ {Pattern} -> GraphExpr |
Example of a Lambda expression.
AddTupleList:: [(Int,Int)] -> [Int]
AddTupleList list = map (\(x,y) = x+y) list
A lambda expression introduces a new scope (see 2.1).
The arguments of the anonymous function being defined have the only a meaning in the corresponding function body.
![]() \ arg1 arg2 ...
argn = function_body
\ arg1 arg2 ...
argn = function_body
3.4.2 Case Expression and Conditional Expression
For programming convenience a case expression and conditional expression are added.
|
CaseExpr |
= |
case GraphExpr of |
|
|
|
{ {CaseAltDef}+ } |
|
|
| |
if BrackGraph BrackGraph BrackGraph |
|
CaseAltDef |
= |
{Pattern} |
|
|
|
{{LetBeforeExpression} |
|
|
|
{| Guard} = [>] FunctionBody}+ |
|
|
|
[LocalFunctionAltDefs] |
|
|
| |
{Pattern} |
|
|
|
{{LetBeforeExpression} |
|
|
|
{| Guard} -> FunctionBody}+ |
|
|
|
[LocalFunctionAltDefs] |
In a case expression first the discriminating expression is evaluated after which the case alternatives are tried in textual order. Case alternatives are similar to function alternatives. This is not so strange because a case expression is internally translated to a function definition (see the example below). Each alternative contains a left-hand side pattern (see 3.2) that is optionally followed by a let-before (see 3.5.4) and a guard (see 3.3). When a pattern matches and the optional guard evaluates to True the corresponding alternative is chosen. A new block structure (scope) is created for each case alternative (see 2.1).
For compatibility with Clean 1.3.x it is also allowed to use the arrow (‘->’) to separate the case alternatives:
The variables defined in the patterns have the only a meaning in the corresponding alternative.
case expression of
![]() pattern1 =
alternative1
pattern1 =
alternative1
![]() pattern2 =
alternative2
pattern2 =
alternative2
![]() ...
...
patternn = alternativen
 All alternatives in the case expression must be of the same type.
All alternatives in the case expression must be of the same type.
 When none of the patterns matches a run-time error is generated.
When none of the patterns matches a run-time error is generated.
The case expression
h x = case g x of
[hd:_] = hd
[] = abort "result of call g x in h is empty"
is semantically equivalent to:
h x = mycase (g x)
where
mycase [hd:_] = hd
mycase [] = abort "result of call g x in h is empty"
In a conditional expression first the Boolean expression is evaluated after which either the then- or the else-part is chosen. The conditional expression can be seen as a simple kind of case expression.
 The then- and else-part in the conditional expression must be of the
same type.
The then- and else-part in the conditional expression must be of the
same type.
 The discriminating expression must be of type Bool.
The discriminating expression must be of type Bool.
3.5 Local Definitions
Sometimes it is convenient to introduce definitions that have a limited scope and are not visible throughout the whole module. One can define functions that have a local scope, i.e. which have only a meaning in a certain program region. Outside the scope the functions are unknown. This locality can be used to get a better program structure: functions that are only used in a certain program area can remain hidden outside that area.
Besides functions one can also convenient to define constant selectors. Constants are named graph expressions (see 3.6).
|
LocalDef |
= |
GraphDef |
|
|
| |
FunctionDef |
3.5.1 Let Expression: Local Definitions in Expressions
A let expression is an expression that enables to introduce a new scope (see 2.1) in an expression in which local functions and constants can be defined. Such local definitions can be introduced anywhere in an expression using a let expression with the following syntax.
|
LetExpresssion |
= |
let { {LocalDef}+ } in GraphExpr |
The function and selectors defined in the let block only have a meaning within the expression.
 let
let
![]() function
arguments = function_body
function
arguments = function_body
selector = expr
...
in expression
Example of a let expression used within a list comprehension.
doublefibs n = [let a = fib i in (a, a) \\ i <- [0..n]]
3.5.2 Where Block: Local Definitions in a Function Alternative
At the end of each function alternative one can locally define functions and constant graphs in a where block.
|
LocalFunctionAltDefs |
= |
[where] { {LocalDef}+ } |
Functions and graphs defined in a where block can be used anywhere in the corresponding function alternative (i.e. in all guards and rule alternatives following a pattern, see 3.1) as indicated in the following picture showing the scope of a where block.
The function and selectors defined in the where block can be used locally in the whole function definition.
function formal_arguments
![]()

![]() | guard1 = function_alternative1
| guard1 = function_alternative1
| guard2 = function_alternative2
| otherwise = default_alternative
where
selector = expr
![]() local_function
args = function_body
local_function
args = function_body
sieve and filter are local functions defined in a where block. They have only a meaning inside primes. At the global level the functions are unknown.
primes::[Int]
primes = sieve [2..]
where
sieve::[Int] -> [Int] // local function of primes
sieve [pr:r] = [pr:sieve (filter pr r)]
filter::Int [Int] -> [Int] // local function of primes
filter pr [n:r]
| n mod pr == 0 = filter pr r
| otherwise = [n:filter pr r]
Notice that the scope rules are such that the formal arguments of the surrounding function alternative are visible to the locally defined functions and graphs. The arguments can therefore directly be addressed in the local definitions. Such local definitions cannot always be typed explicitly (see 3.7).
Alternative definition of primes. The function filter is locally defined for sieve. filter can directly access arguments pr of sieve.
primes::[Int]
primes = sieve [2..]
where
sieve::[Int] -> [Int] // local function of primes
sieve [pr:r] = [pr:sieve (filter r)]
where
filter::[Int] -> [Int] // local function of sieve
filter [n:r]
| n mod pr == 0 = filter r
| otherwise = [n:filter r]
3.5.3 With Block: Local Definitions in a Guarded Alternative
One can also locally define functions and graphs at the end of each guarded rule alternative using a with block.
|
LocalFunctionDefs |
= |
[with] { {LocalDef}+ } |
|
LocalDef |
= |
GraphDef |
|
|
| |
FunctionDef |
Functions and graphs defined in a with block can only be used in the corresponding rule alternative as indicated in the following picture showing the scope of a with block.
The function and selectors defined in the with block can be locally only be used in the corresponding function alternative.

 function formal arguments
function formal arguments
| guard1 = function_alternative1
with
selector = expr

![]() local_function args = function_body
local_function args = function_body
| guard2 = function_alternative2
with
selector = expr
![]() local_function args = function_body
local_function args = function_body
Notice that the scope rules are such that the arguments of the surrounding guarded rule alternative are visible to the locally defined functions and graphs. The arguments can therefore directly be addressed in the local definitions. Such local definitions cannot always be typed explicitly (see 3.7).
3.5.4 Let-Before Expression: Local Constants defined between Guards
Many of the functions for input and output in the Clean I/O library are state transition functions. Such a state is often passed from one function to another in a single threaded way (see Chapter 9) to force a specific order of evaluation. This is certainly the case when the state is of unique type. The threading parameter has to be renamed to distinguish its different versions. The following example shows a typical example:
Use of state transition functions. The uniquely typed state file is passed from one function to another involving a number of renamings: file, file1, file2)
readchars:: *File -> ([Char], *File)
readchars file
| not ok = ([],file1)
| otherwise = ([char:chars], file2)
where
(ok,char,file1) = freadc file
(chars,file2) = readchars file1
This explicit renaming of threaded parameters not only looks very ugly, these kind of definitions are sometimes also hard to read as well (in which order do things happen? which state is passed in which situation?). We have to admit: an imperative style of programming is much easier to read when things have to happen in a certain order such as is the case when doing I/O. That is why we have introduced let-before expressions.
Let-before expressions are special let expressions that can be defined before a guard or function body. In this way one can specify sequential actions in the order in which they suppose to happen. Let-before expressions have the following syntax:
|
LetBeforeExpression |
= |
# {GraphDef}+ |
|
|
| |
#!{GraphDef}+ |
The form with the exclamation mark (#!) forces the evaluation of the node-ids that appear in the left-hand sides of the definitions. Notice that one can only define constant selectors (GraphDef) in a Let-before expression. One cannot define functions.
Let-before expressions have a special scope rule to obtain an imperative programming look. The variables in the left-hand side of these definitions do not appear in the scope of the right-hand side of that definition, but they do appear in the scope of the other definitions that follow (including the root expression, excluding local definitions in where blocks.
This is shown in the following picture:

Function args
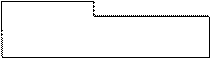 # selector1 = expression1
# selector1 = expression1
| guard1 = expression2
![]() #
selector2 = expression3
#
selector2 = expression3
| guard2 = expression4
where
local_definitions
Notice that a variable defined in a let-before expression cannot be used in a where expression. The reverse is true however: definitions in the where expression can be used in the let before expression.
Use of let before expressions, short notation, re-using names taking use of the special scope of the let before)
readchars:: *File -> ([Char], *File)
readchars file
# (ok,char,file) = freadc file
| not ok = ([],file)
# (chars,file) = readchars file
= ([char:chars], file)
Equivalent definition renaming threaded parameters)
readchars:: *File -> ([Char], *File)
readchars file
# (ok,char,file1) = freadc file
| not ok = ([],file1)
# (chars, file2) = readchars file1
= ([char:chars], file2)
The notation can also be dangerous: the same name is used on different spots while the meaning of the name is not always the same (one has to take the scope into account which changes from definition to definition). However, the notation is rather safe when it is used to thread parameters of unique type. The type system will spot it when such parameters are not used in a correct single threaded manner. We do not recommend the use of let before expressions to adopt an imperative programming style for other cases.
Abuse of let before expression.
exchange:: (a, b) -> (b, a)
exchange (x, y)
# temp = x
x = y
y = temp
= (x, y)
3.6 Defining Constants
One can give a name to a constant expression (actually a graph), such that the expression can be used in (and shared by) other expressions. One can also identify certain parts of a constant via a projection function called a selector (see below).
|
GraphDef |
= |
Selector =[:] GraphExpr ; |
Graph locally defined in a function: the graph labeled last is shared in the function StripNewline and computed only once.
StripNewline:: String -> String
StripNewline "" = ""
StripNewline string
| string !! last<>'\n' = string
| otherwise = string%(0,last-1)
where
last = maxindex string
When a graph is defined actually a name is given to (part) of an expression. The definition of a graph can be compared with a definition of a constant (data) or a constant (projection) function. However, notice that graphs are constructed according to the basic semantics of Clean (see Chapter 1) that means that multiple references to the same graph will result in sharing of that graph. Recursive references will result in cyclic graph structures. Graphs have the property that they are computed only once and that their value is remembered within the scope they are defined in.
Graph definitions differ from constant function definitions. A constant function definition is just a function defined with arity zero (see 3.1). A constant function defines an ordinary graph rewriting rule: multiple references to a function just means that the same definition is used such that a (constant) function will be recomputed again for each occurrence of the function symbol made. This difference can have consequences for the time and space behavior of function definitions (see 10.2).
The Hamming numbers defined using a locally defined cyclic constant graph and defined by using a globally defined recursive constant function. The first definition (ham1) is efficient because already computed numbers are reused via sharing. The second definition (ham2 ) is much more inefficient because the recursive function recomputes everything.
ham1:: [Int]
ham1 = y
where y = [1:merge (map ((*) 2) y) (merge (map ((*) 3) y) (map ((*) 5) y))]
ham2:: [Int]
ham2 = [1:merge (map ((*) 2) ham2) (merge (map ((*) 3) ham2) (map ((*) 5) ham2 ))]
Syntactically the definition of a graph is distinguished from the definition of a function by the symbol which separates left-hand side from right-hand side: "=:" is used for graphs while "=>" is used for functions. However, in general the more common symbol "=" is used for both type of definitions. Generally it is clear from the context what is meant (functions have parameters, selectors are also easy recognisible). However, when a simple constant is defined the syntax is ambiguous (it can be a constant function definition as well as a constant graph definition).
To allow the use of the "=" whenever possible, the following rule is followed. Local constant definitions are by default taken to be graph definitions and therefore shared, globally they are by default taken to be function definitions (see 3.1) and therefore recomputed. If one wants to obtain a different behavior one has to explicit state the nature of the constant definition (has it to be shared or has it to be recomputed) by using "=:" (on the global level, meaning it is a constant graph which is shared) or "=>" (on the local level, meaning it is a constant function and has to be recomputed).
Local constant graph versus local constant function definition: biglist1 and biglist2 is a graph which is computed only once, biglist3 is a constant function which is computed every time it is applied.
biglist1 = [1..10000] // a graph (if defined locally)
biglist1 = [1..10000] // a constant function (if defined globally)
biglist2 =: [1..10000] // a graph (always)
biglist3 => [1..10000] // a constant function (always)
The garbage collector will collect locally defined graphs when they are no longer connected to the root of the program graph (see Chapter 1).
3.6.1 Selectors
The left-hand side of a graph definition can be a simple name, but is can also be a more complicated pattern called a selector. A selector is a pattern which introduces one or more new selector variables implicitly defining projection functions to identify (parts of) a constant graph being defined One can identify the sub-graph as a whole or one can identify its components. A selector can contain constants (also user defined constants introduced by algebraic type definitions), variables and wildcards. With a wildcard one can indicate that one is not interested in certain components.
Selectors cannot be defined globally. They can only locally be defined in a let (see 3.5.1), a let-before (see 3.5.4), a where-block (see 3.5.2), and a with-block (see 3.5.3). Selectors can furthermore appear on the left-hand side of generators in list comprehensions (see 4.2.1) and array comprehensions (see 4.4.1).
|
Selector |
= |
BrackPattern |
Use of a selector to locally select tuple elements.
unzip::[(a,b)] -> ([a],[b])
unzip [] = ([],[])
unzip [(x,y):xys] = ([x:xs],[y:ys])
where
(xs,ys) = unzip xys
 When
a selector on the left-hand side of a graph definition is not matching the graph
on the right-hand side it will result in a run-time error.
When
a selector on the left-hand side of a graph definition is not matching the graph
on the right-hand side it will result in a run-time error.
 The selector variables introduced in the selector must be different
from each other and not already be used in the same scope and name space (see 1.2).
The selector variables introduced in the selector must be different
from each other and not already be used in the same scope and name space (see 1.2).
 To avoid the specification of patterns that may fail at run-time, it
is not allowed to test on zero arity constructors. For instance, list used in a
selector pattern need to be of form [a:_]. [a] cannot be used because
it stands for [a:[]] implying a test on the zero arity constructor []. If the
pattern is a record only those fields which contents one is interested in need
to be indicated in the pattern
To avoid the specification of patterns that may fail at run-time, it
is not allowed to test on zero arity constructors. For instance, list used in a
selector pattern need to be of form [a:_]. [a] cannot be used because
it stands for [a:[]] implying a test on the zero arity constructor []. If the
pattern is a record only those fields which contents one is interested in need
to be indicated in the pattern
 Arrays cannot be used as pattern in a selector.
Arrays cannot be used as pattern in a selector.
 Selectors cannot be defined globally.
Selectors cannot be defined globally.
3.7 Typing Functions
Although one is in general not obligated to explicitly specify the type of a function (the Clean compiler can in general infer the type) the explicit specification of the type is highly recommended to increase the readability of the program.
|
FunctionDef |
= |
[FunctionTypeDef] |
|
|
|
DefOfFunction |
|
|
|
|
|
FunctionTypeDef |
= |
FunctionName :: FunctionType ; |
|
|
| |
(FunctionName) [Fix][Prec] [:: FunctionType] ; |
|
Fix |
= |
infixl |
|
|
| |
infixr |
|
|
| |
infix |
|
Prec |
= |
Digit |
|
FunctionType |
= |
Type -> Type [ClassContext] [UnqTypeUnEqualities] |
|
Type |
= |
{BrackType}+ |
|
BrackType |
= |
[UniversalQuantVariables] [Strict] [UnqTypeAttrib] SimpleType |
|
UniversalQuantVariables |
= |
A.{TypeVariable }+: |
An explicit specification is required when a function is exported, or when the programmer wants to impose additional restrictions on the application of the function (e.g. a more restricted type can be specified, strictness information can be added as explained in Chapter 10.1, a class context for the type variables to express overloading can be defined as explained in Chapter 7, uniqueness information can be added as explained in 3.7.53.7.5 Functions with Strict Arguments).
The Clean type system uses a combination of Milner/Mycroft type assignment. This has as consequence that the type system in some rare cases is not capable to infer the type of a function (using the Milner/Hindley system) although it will approve a given type (using the Mycroft system; see Plasmeijer and Van Eekelen, 1993). Also when universally quantified types of rank 2 are used (see 3.7.4), explicit typing by the programmer is required.
The Cartesian product is used for the specification of the function type. The Cartesian product is denoted by juxtaposition of the bracketed argument types. For the case of a single argument the brackets can be left out. In type specifications the binding priority of the application of type constructors is higher than the binding of the arrow ->. To indicate that one defines an operator the function name is on the left-hand side surrounded by brackets.
 The function symbol before the double colon should be the same as
the function symbol of the corresponding rewrite rule.
The function symbol before the double colon should be the same as
the function symbol of the corresponding rewrite rule.
 The arity of the functions has to correspond with the number of
arguments of which the Cartesian product is taken. So, in Clean one can tell the arity of the function by its type.
The arity of the functions has to correspond with the number of
arguments of which the Cartesian product is taken. So, in Clean one can tell the arity of the function by its type.
Showing how the arity of a function is reflected in type.
map:: (a->b) [a] -> [b] // map has arity 2
map f [] = []
map f [x:xs] = [f x : map f xs]
domap:: ((a->b) [a] -> [b]) // domap has arity zero
domap = map
 The arguments and the result types of a function should be of kind X.
The arguments and the result types of a function should be of kind X.
 In the specification of a type of a locally defined function one
cannot refer to a type variable introduced in the type specification of a
surrounding function (there is not yet a scope rule on types defined). The
programmer can therefore not specify the type of such a local function.
However, the type will be inferred and checked (after it is lifted by the
compiler to the global level) by the type system.
In the specification of a type of a locally defined function one
cannot refer to a type variable introduced in the type specification of a
surrounding function (there is not yet a scope rule on types defined). The
programmer can therefore not specify the type of such a local function.
However, the type will be inferred and checked (after it is lifted by the
compiler to the global level) by the type system.
Counter example (illegal type specification). The function g returns a tuple. The type of the first tuple element is the same as the type of the polymorphic argument of f. Such a dependency (here indicated by “^” cannot be specified).
f:: a -> (a,a)
f x = g x
where
// g:: b -> (a^,b)
g y = (x,y)
3.7.1 Typing Curried Functions
In Clean all symbols (functions and constructors) are defined with fixed arity. However, in an application it is of course allowed to apply them to an arbitrary number of arguments. A curried application of a function is an application of a function with a number of arguments which is less than its arity (note that in Clean the arity of a function can be derived from its type). With the aid of the predefined internal function _AP a curried function applied on the required number of arguments is transformed into an equivalent uncurried function application.
The type axiom’s of the Clean type system include for all s defined with arity n the equivalence of s::(t1->(t2->(…(tn->tr)…)) with s::t1 t2 … tn -> tr.
3.7.2 Typing Operators
An operator is a function with arity two that can be used in infix position. An operator can be defined by enclosing the operator name between parentheses in the left-hand-side of the function definition. An operator has a precedence (0 through 9, default 9) and a fixity (infixl, infixr or just infix, default infixl). A higher precedence binds more tightly. When operators have equal precedence, the fixity determines the priority. In an expression an ordinary function application always has the highest priority (10). See also Section 3.1 and 3.4.
 The type of an operator must obey the requirements as defined for
typing functions with arity two.
The type of an operator must obey the requirements as defined for
typing functions with arity two.
 If the operator is explicitly typed the operator name should also
be put between parentheses in the type rule.
If the operator is explicitly typed the operator name should also
be put between parentheses in the type rule.
 When an infix operator is enclosed between parentheses it can be
applied as a prefix function. Possible recursive definitions of the newly
defined operator on the right-hand-side also follow this convention.
When an infix operator is enclosed between parentheses it can be
applied as a prefix function. Possible recursive definitions of the newly
defined operator on the right-hand-side also follow this convention.
Example of an operator definition and its type.
(o) infix 8:: (x -> y) (z -> x) -> (z -> y) // function composition
(o) f g = \x -> f (g x)
3.7.3 Typing Partial Functions
Patterns and guards imply a condition that has to be fulfilled before a rewrite rule can be applied (see 3.2 and 3.3). This makes it possible to define partial function s, functions which are not defined for all possible values of the specified type.
 When a partial function is applied to a value outside the domain for
which the function is defined it will result into a run-time error. The
compiler gives a warning when functions are defined which might be partial.
When a partial function is applied to a value outside the domain for
which the function is defined it will result into a run-time error. The
compiler gives a warning when functions are defined which might be partial.
With the abort expression (see StdMisc.dcl) one can change any partial function into a total function (the abort expression can have any type). The abort expression can be used to give a user-defined run-time error message
Use of abort to make a function total.
fac:: Int -> Int
fac 0 = 1
fac n
| n>=1 = n * fac (n - 1)
| otherwise = abort "fac called with a negative number"
3.7.4 Explicit use of the Universal Quantifier in Function Types
When a type of a polymorphic function is specified in Clean, the universal quantifier is generally left out.
The function map defined as usual, no universal quantifier is specified:
map:: (a->b) [a] -> [b]
map f [] = []
map f [x:xs] = [f x : map f xs]
Counter Example. The same function map again, but now the implicit assumed universal quantifier has been made visible. It shows the meaning of the specified type more precisely, but is makes the type definition a bit longer as well. The current version of Clean does not yet allow universal quantifiers on the topmost level !!
map:: A.a b:(a->b) [a] -> [b]
map f [] = []
map f [x:xs] = [f x : map f xs]
Not yet Implemented: In Clean 2.0 it is allowed to explicitly write down the universal quantifier. One can write down the qualifier A. (for all) direct after the :: in the type definition of a function. In this way one can explicitly introduce the type variables used in the type definition of the function. As usual, the type variables thus introduced have the whole function type definition as scope.
|
= |
Type -> Type [ClassContext] [UnqTypeUnEqualities] |
|
|
Type |
= |
{BrackType}+ |
|
BrackType |
= |
[UniversalQuantVariables] [Strict] [UnqTypeAttrib] SimpleType |
|
UniversalQuantVariables |
= |
A.{TypeVariable }+: |
Implemented: Clean 2.0 offers Rank 2 polymorphism: it is also possible to specify the universal quantifier with as scope the type of an argument of a function or the type of the result of a function. This makes it possible to pass polymorphic functions as an argument to a function which otherwise would be treated monomorphic. The advantage of the use of Rank 2 polymorphism is that more programs will be approved by the type system, but one explicitly (by writing down the universal quantifier) has to specify in the type of function that such a polymorphic function is expected as argument or delivered as result.
Not yet Implemented: We will allow Rank N polymorphism. We are working on it.
Example: The function h is used to apply a polymorphic function of type (A.a: [a] -> Int) to a list of Int as well as a list of Char. Due to the explicit use of the universal quantifier in the type specification of h this definition is approved.
h:: (A.a: [a] -> Int) -> Int
h f = f [1..100] + f ['a'..'z']
Start = h length
Counter Example: The function h2 is used to apply a function of type ([a] -> Int) to a list of Int as well as a list of Char. In this case the definition is rejected due to a type unification error. It is assumed that the argument of h2 is unifiable with [a] -> Int, but it is not assumed that the argument of h2 is (A.a: [a] -> Int). So, the type variable a is unified with both Int and Char, which gives rise to a type error.
h2:: ([a] -> Int) -> Int
h2 f = f [1..100] + f ['a'..'z']
Start = h2 length
Counter Example: The function h3 is used to apply a function to a list of Int as well as a list of Char. Since no type is specified the type inference system will assume f to be of type ([a] -> Int) but not of type (A.a: [a] -> Int). The situation is the same as above and we will again get a type error.
h3 f = f [1..100] + f ['a'..'z']
Start = h3 length
 Clean cannot infer polymorphic functions of Rank 2 automatically! One is
obligated to explicitly specify universally quantified types of Rank 2.
Clean cannot infer polymorphic functions of Rank 2 automatically! One is
obligated to explicitly specify universally quantified types of Rank 2.
 Explicit universal quantification on higher ranks than rank 2 (e.g.
quantifiers specified somewhere inside the type specification of a function
argument) is not allowed.
Explicit universal quantification on higher ranks than rank 2 (e.g.
quantifiers specified somewhere inside the type specification of a function
argument) is not allowed.
 A polymorphic function of Rank 2 cannot be used in a curried way for
those arguments in which the function is universally quantified.
A polymorphic function of Rank 2 cannot be used in a curried way for
those arguments in which the function is universally quantified.
Counter Examples: In the example below it is shown that f1 can only be used when applied to all its arguments since its last argument is universally quantified. The function f2 can be used curried only with respect to its last argument that is not universally quantified.
f1:: a (A.b:b->b) -> a
f1 x id = id x
f2:: (A.b:b->b) a -> a
f2 id x = id x
illegal1 = f1 // this will raise a type error
illegal2 = f1 3 // this will raise a type error
legal1 :: Int
legal1 = f1 3 id where id x = x // ok
illegal3 = f2 // this will raise a type error
legal2 :: (a -> a)
legal2 = f2 id where id x = x // ok
legal3 :: Int
legal3 = f2 id 3 where id x = x // ok
3.7.5 Functions with Strict Arguments
In the type definition of a function the arguments can optionally be annotated as being strict. In reasoning about functions it will always be true that the corresponding arguments will be in strong root normal form (see 2.1) before the rewriting of the function takes place. In general, strictness information will increase the efficiency of execution (see Chapter 10).
|
FunctionType |
= |
Type -> Type [ClassContext] [UnqTypeUnEqualities] |
|
Type |
= |
{BrackType}+ |
|
BrackType |
= |
[UniversalQuantVariables] [Strict] [UnqTypeAttrib] SimpleType |
Example of a function with strict annotated arguments.
Acker:: !Int !Int -> Int
Acker 0 j = inc j
Acker i 0 = Acker (dec i) 1
Acker i j = Acker (dec i) (Acker i (dec j))
The Clean compiler includes a fast and clever strictness analyzer that is based on abstract reduction (Nöcker, 1993). The compiler can derive the strictness of the function arguments in many cases, such as for the example above. Therefore there is generally no need to add strictness annotations to the type of a function by hand. When a function is exported from a module (see Chapter 2), its type has to be specified in the definition module. To obtain optimal efficiency, the programmer should also include the strictness information to the type definition in the definition module. One can ask the compiler to print out the types with the derived strictness information and paste this into the definition module.
 Notice that strictness annotations are only allowed at the outermost
level of the argument type. Strictness annotations inside type instances of
arguments are not possible (with exception for some predefined types like
tuples and lists). Any (part of) a data structure can be changed from lazy to
strict, but this has to be specified in the type definition (see 5.1.5).
Notice that strictness annotations are only allowed at the outermost
level of the argument type. Strictness annotations inside type instances of
arguments are not possible (with exception for some predefined types like
tuples and lists). Any (part of) a data structure can be changed from lazy to
strict, but this has to be specified in the type definition (see 5.1.5).